Interactive Educational Modules in
Scientific Computing

Picard Iteration

This module illustrates Picard iteration for solving an initial value problem for an ordinary differential equation. Picard iteration generates a solution of an initial value problem for an ordinary differential equation (ODE) using fixed-point iteration. Picard iteration is used mainly as a theoretical tool to prove the existence of a solution, but it can be implemented numerically, as demonstrated in this module. Given an ODE y′ = f(t, y) with initial condition y(t₀) = y₀, if we integrate both sides of the ODE and use the initial condition, we obtain the integral equation

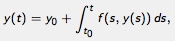
which must be satisfied by the solution y of the initial value problem. Solving the ODE thus appears to have become a quadrature problem, except that we don't know the value of y on the right-hand side. This integral equation formulation is set up naturally for fixed-point iteration, however, plugging a guess for y into the right-hand side to obtain a new value for y and then repeating. Starting with the constant function y₀(t) = y₀, Picard iteration is given by

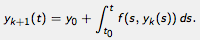
If the function f satisfies a Lipschitz condition, then it can be shown that there is an interval about t₀ in which Picard iteration converges to a solution y of the initial value problem. To implement Picard iteration numerically, the required integrals can be computed using a composite quadrature rule.

The user begins by selecting a differential equation from the menu provided. The exact solution curve through a predefined initial value is drawn in black, and the constant starting function for Picard iteration (based on the prescribed initial value) is drawn in blue. The user also selects a quadrature rule from the menu provided and a value for the mesh spacing of the composite quadrature using the slider. Each time the user clicks Iterate, a Picard iteration is performed and the resulting new approximate solution is added to the graph. Successive approximate solutions are color coded from blue to red as iterations proceed. Note that the interval in which Picard iteration converges to the true solution does not always extend across the entire range shown.

Reference: R. M. M. Mattheij and J. Molenaar, Ordinary Differential Equations in Theory and Practice, John Wiley & Sons, New York, 1996 (reprinted by SIAM, 2002). See pages 30-31.

Developers: Evan VanderZee and Michael Heath