Galerkin Method
This module enables the user to compare different approximate
solutions computed using the Galerkin method for boundary value
problems for ordinary differential equations. A general boundary value
problem (BVP) consists of an ordinary differential equation
(ODE) with side conditions specified at more than one point.
This module illustrates the solution of second-order scalar ODEs of the
form u″ = f(t, u,
u′) on an interval [a,
b] with boundary conditions u(a) =
α and u(b) =
β. The Galerkin method approximates the
solution to the BVP by a linear combination of basis functions
determined by requiring that the residual be orthogonal to each of the
homogeneous basis functions, i.e., those that vanish on the boundary,
and that the boundary conditions be satisfied. Let
φ1,…,φn
be a set of basis functions. We will approximate the solution to the
boundary value problem by a linear combination v(t,
x) = x1
φ1(t) + · · · +
xn
φn(t) of the basis
functions, where the vector x of coefficents is to be
determined. The coefficients of the homogeneous basis functions (i.e.,
φi(a) =
φi(b) = 0) are determined by
an orthogonality condition, while the coefficients of the inhomogeneous
basis functions are chosen to satisfy the boundary conditions. The
orthogonality condition requires that for each homogeneous basis
function φi,
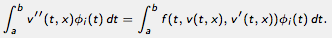
Integrating the left side by parts and using homogeneity, we can
replace v″(t, x)
φi(t) by
−v′(t, x)
φi′(t), which lowers
the differentiability requirements on the basis functions. The result
is a system of equations that can be solved for the coefficients
x of the approximate solution v(t,
x). This system of equations will be nonlinear if the
function f is nonlinear. The necessary integrals can be
evaluated by numerical quadrature, and the accuracy of the solution
will be affected by the accuracy of this numerical integration.
The user begins by selecting from the menu provided an ODE and a
specific solution to be sought (if there is more than one). Boundary
values u(a) = α and
u(b) = β are indicated by black
dots on the graph. Next the user chooses a type and number of basis
functions to be used. The available bases are piecewise polynomials
with equally spaced breakpoints in the interval [a,
b]. The user also chooses a quadrature method for
evaluating the integrals. When the user clicks Solve the
resulting approximate solution to the BVP is drawn on the graph. To
compare this solution with other approximate solutions, the user can
make additional choices of basis functions, number of mesh points, and
quadrature rules, then click Solve to add each new approximate
solution to the graph. The solutions for different parameters are
color coded so that the color changes from blue to red as the number of
mesh points increases and from light to dark as the order of the
quadrature rule increases. For each quadrature rule, the solutions get
slightly darker as the selected basis changes from Hat Function
to Quadratic Element to Quadratic Spline. To clear all
of the solutions from the graph, click Reset.
To illustrate the details of the individual steps of the Galerkin
method for a particular choice of parameters, see the alternative
Galerkin Method module.
Reference:
Michael T. Heath, Scientific Computing,
An Introductory Survey, 2nd edition, McGraw-Hill, New York,
2002. See Section 10.6.
Developers: Evan VanderZee and Michael Heath