Interactive Educational Modules
in
Scientific Computing
Vector p-Norms
This module graphically illustrates vector
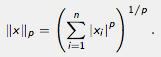 Important special cases include
Important special cases include
-
Manhattan norm, the distance between two points measured in
“city blocks”, given by
p = 1 -
Euclidean norm, the usual notion of distance in Euclidean
space, given by
p = 2 -
Infinity or max norm, given by the limit as
p → ∞ ,

For any given norm, the unit circle is the set of all points
having norm 1, although it is a circle in the conventional sense only
for
The user first selects a vector by clicking on the graph. The
vector selected is shown by an arrow in the graph and also by its
numerical coordinates in the right panel. The user then selects a
value for p from the menu provided. To determine the
Reference: Michael T. Heath, Scientific Computing, An Introductory Survey, 2nd edition, McGraw-Hill, New York, 2002. See Section 2.3.1 and Figure 2.2.
Developers: Sukolsak Sakshuwong and Michael Heath
