Interactive Educational Modules
in
Scientific Computing
Error Bound
This module graphically illustrates a standard bound on the relative
error in the solution vector x to a system of linear equations
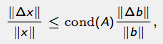 where the condition number
of the matrix is defined by
where the condition number
of the matrix is defined by
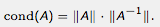 A similar bound applies for perturbations in the matrix
A, but for this module we will consider only
perturbations in the right-hand-side vector b. For this
module we will use the Euclidean 2-norm in
two dimensions.
A similar bound applies for perturbations in the matrix
A, but for this module we will consider only
perturbations in the right-hand-side vector b. For this
module we will use the Euclidean 2-norm in
two dimensions.
Such an error bound is important because there is usually some level of uncertainty in the problem data, for example due to measurement error or rounding error. Because of this uncertainty, the right-hand-side vector b is perhaps better thought of as a fuzzy region rather than as a single well-defined point, and thus the corresponding solution vector x is also a fuzzy region rather than a single point. The error bound cited above gives some idea of the size of the region of uncertainty in which the solution vector x lies for a given level of relative uncertainty in b. We will see that the bound can be tight or loose, depending on the particular matrix A and vector b.
The user first selects a matrix A by entering values for its entries in the text boxes or using a preset example. Next the user selects a right-hand-side vector b by clicking on the right graph. The vector b selected is shown by an arrow at the selected location in the right graph and also by its numerical coordinates below. The vector b can be dragged to a new location at any time, if desired. The corresponding solution vector x is shown by an arrow in the left graph and also by its numerical coordinates below.
The region of uncertainty in the right-hand-side vector b for a given relative error is shown in the right graph by a shaded circular disk whose size can be altered by dragging its perimeter, and the resulting numerical value for the relative error in b is shown below. The lightly shaded circular disk in the left graph shows the corresponding region of uncertainty in the solution vector x given by the condition number of the matrix, and the corresponding bound on the relative error in x is shown below. In addition, the actual preimage of the disk on the right is shown by the darkly shaded ellipse in the left graph, and the corresponding actual worst case relative error in x is shown below. The circular disk on the left always contains this ellipse, but the bound may be tight or loose, depending on the particular choice of matrix A and right-hand-side vector b. The vectors can be reset by clicking Clear, and the matrix can be changed by entering new values for its entries.
Reference: Michael T. Heath, Scientific Computing, An Introductory Survey, 2nd edition, McGraw-Hill, New York, 2002. See Section 2.3.4.
Developers: Sukolsak Sakshuwong and Michael Heath
