Bernstein Polynomial Approximation
This module illustrates Bernstein polynomial approximation. The
Weierstrass approximation theorem states that for any continuous
function f on a closed interval, say [0, 1], and
any ε > 0, there is a polynomial p such that
for any x in [0, 1], | f (x)
− p(x) | < ε. Russian
mathematician Serge Bernstein gave a constructive proof of this theorem
in 1912 by explicitly producing a sequence of polynomials
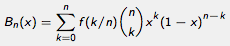
that converge uniformly to f as n increases,
where the binomial coefficient
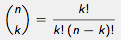
is the number of distinct ways a set of k objects can be chosen
from a set of n objects (“n choose
k”). By shifting and scaling, the Bernstein polynomials
Bn(x) can be used to approximate a
function f on any closed interval [a,
b]. The convergence of Bernstein polynomials is too slow
for many practical approximation purposes, but they enjoy certain
monotonicity and shape-preserving properties that make them useful, for
example, in computer graphics. One such application is a compact
representation of Bezier curves.
The user begins by selecting a function f(x)
from the list of available functions, and the graph
of the selected function is drawn in black. Repeatedly clicking
Next causes Bernstein polynomial approximations of increasing
degree to be added to the graph. The color of the approximating
polynomials changes from blue to red as the degree increases, and the
polynomial written below the graph is updated to reflect the
coefficients of the highest degree Bernstein polynomial shown.
Reference: George M. Phillips, Interpolation and
Approximation by Polynomials, Springer, New York, 2003. See Chapter
7, pages 247-290.
Developers: Evan VanderZee and Michael Heath
